Factorization with Zero Divisors
Historically, the study of nonunique factorization was motivated by attempts to solve Fermat's last theorem, namely the incorrect assumption that if you adjoin a complex primitive root of unity to the rationals Q, a UFD, the resulting ring extension is also a UFD, that is, a ring where every nonzero nonunit can be factored uniquely in the product of atoms. This led to an interest in properties weaker than unique factorization. For example, a half-factorial domain (HFD) is a domain in which every nonzero nonunit element has a factorization into atoms of the same length. A UFD has a class number of 1, whereas an HFD has a class number of 2. While number theorists were content to focus on these two factorization properties, in Factorization in Integral Domains Anderson et. al. introduced a number of properties progressively weaker than unique factorization such as finite factorization (FF), bounded factorization (BF), ACCP, and atomic. This work was followed by Factorization in Commutative Rings with Zero Divisors by Anderson et. al. which extended the study of nonunique factorization to arbitrary commutative rings.
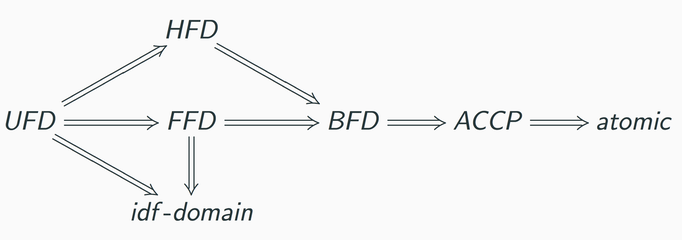
The figures below highlight the relationship between certain factorization properties in the domain case and in the case where R is an arbitrary commutative ring. An arrow from one property to another means that the first property implies the second, for example if R has the unique factorization property it also has the half-factorial property. None of the arrows can be reversed.
My research focuses on how factorization properties behave with respect to certain extensions. Of particular interest is the extension of a commutative ring R with identity to the polynomial ring extension R[X]: if one of these rings has a certain factorization property, does the other?
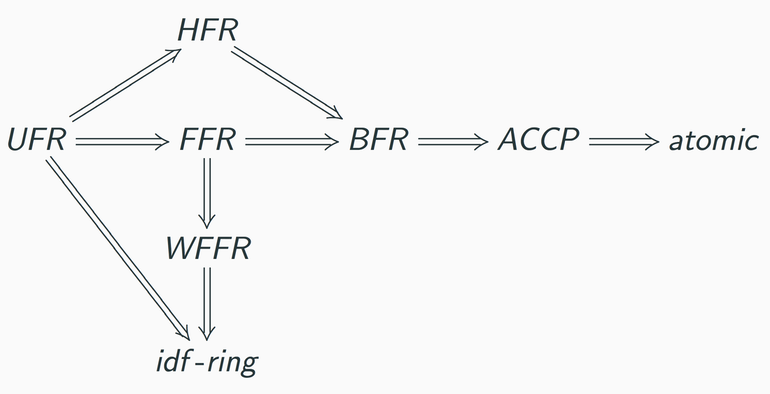
The figures below highlight the relationship between certain factorization properties in the domain case and in the case where R is an arbitrary commutative ring. An arrow from one property to another means that the first property implies the second, for example if R has the unique factorization property it also has the half-factorial property. None of the arrows can be reversed.
My research focuses on how factorization properties behave with respect to certain extensions. Of particular interest is the extension of a commutative ring R with identity to the polynomial ring extension R[X]: if one of these rings has a certain factorization property, does the other?
Selected Works
Unique Factorization in Polynomial Rings with Zero Divisors (with D.D. Anderson)
In this work we surveyed unique factorization in commutative rings with zero divisors, and gave a complete characterization of when a polynomial ring over an arbitrary commutative ring has some form unique factorization, and determined which forms of unique factorization of R extended to the polynomial ring R[X]. We also discussed irreducible elements of R[X] and provided results on the factorization of powers of an indeterminate X over a commutative ring R.
We were able to show that X is a product of irreducible elements (resp., principal primes) if and only if R is a finite direct product of indecomposable rings (resp., integral domains). In the case where X is a product of irreducibles, this factorization is unique up to order and associates while each power of X^n has unique factorization into irreducibles if and only if R is reduced and a finite direct product of indecomposable rings.
In this work we surveyed unique factorization in commutative rings with zero divisors, and gave a complete characterization of when a polynomial ring over an arbitrary commutative ring has some form unique factorization, and determined which forms of unique factorization of R extended to the polynomial ring R[X]. We also discussed irreducible elements of R[X] and provided results on the factorization of powers of an indeterminate X over a commutative ring R.
We were able to show that X is a product of irreducible elements (resp., principal primes) if and only if R is a finite direct product of indecomposable rings (resp., integral domains). In the case where X is a product of irreducibles, this factorization is unique up to order and associates while each power of X^n has unique factorization into irreducibles if and only if R is reduced and a finite direct product of indecomposable rings.
Associates, Irreducibility, and Factorization Length in Monoid Rings with Zero Divisors (with Jason Juett)
Monoid rings generalize both monoid domains and polynomial rings with zero divisors. Let R be a ring and S a monoid. We write the elements of the monoid ring R[S] as ``polynomials" with coefficients in R and exponents in S. It is possible for R[S] to have zero divisors, even if R is a domain. For example if we take R=Z (integers) and S=Z/2Z (integers modulo 2), then in Z[S] we have that (x+1)(x-1)=x^2-1=1-1=0. Factorization in R[S] is somewhat well known, but is relatively unexplored in the case where R can possibly contain zero divisors.
In this work we studied associate relations and the resulting notions of irreducibility and factorization length in monoid rings with zero divisors. We characterized monoid rings that are bounded factorization rings (BFRs) or satisfy the ascending chain condition on principal ideals (ACCP). We also characterized the monoid rings that are presimplifiable or domainlike. Many of these results concerned monoid rings R[S] where S was torsion-free cancellative.
Monoid rings generalize both monoid domains and polynomial rings with zero divisors. Let R be a ring and S a monoid. We write the elements of the monoid ring R[S] as ``polynomials" with coefficients in R and exponents in S. It is possible for R[S] to have zero divisors, even if R is a domain. For example if we take R=Z (integers) and S=Z/2Z (integers modulo 2), then in Z[S] we have that (x+1)(x-1)=x^2-1=1-1=0. Factorization in R[S] is somewhat well known, but is relatively unexplored in the case where R can possibly contain zero divisors.
In this work we studied associate relations and the resulting notions of irreducibility and factorization length in monoid rings with zero divisors. We characterized monoid rings that are bounded factorization rings (BFRs) or satisfy the ascending chain condition on principal ideals (ACCP). We also characterized the monoid rings that are presimplifiable or domainlike. Many of these results concerned monoid rings R[S] where S was torsion-free cancellative.
Numerical Semigroup Algebras
A numerical semigroup is a subset S of the natural numbers that is closed under addition, has finite complement, and contains zero. Every numerical semigroup admits a unique generating set, and when we write S=< n1,...,nk> we assume n1,...,nk are minimal generators of S. The smallest nontrivial numerical semigroup is S=<2,3>, which includes all linear combinations of the generators 2 and 3, for example, 23 is in S since 23=2*4+ 3*5. In this case S includes all natural numbers except 1. We call a a gap of a numerical semigroup if a is not in S, and the largest gap is called the Frobenius number of S. In the case S=<2,3>, the Frobenius number F(S)=1. Given a numerical semigroup S and a field k, we can form the numerical semigroup algebra k[S] which consists only of terms x^i with i in S. For example, the numerical semigroup algebra k[S] where k=Z/2Z (integers modulo 2) and S=<2,3> does not contain linear polynomials since 1 is not in S. Semigroup algebras, when viewed as quotients of toric ideals, are central to combinatorial commutative algebra, and arise in a host of statistical and computational applications.
Selected Works
On Atomic Density in Numerical Semigroup Algebras (with Austin Antoniou, Bethany Kubik, Christopher O'Neill, and Shannon Talbott)
In this work we initiated the study of atomic density in numerical semigroup algebras, which is the limiting value of the ratio of irreducibles of degree n to total polynomials of degree n for some numerical semigroup algebra over a finite field. Numerical semigroup algebras exhibit non unique factorization, and it is of interest to see what is happening to the number of irreducibles of a given degree n as n grows larger. The main result of this paper is that any numerical semigroup algebra has atomic density 0. This means that for a given numerical semigroup algebra S over a finite field k, in some sense, `most' polynomials in k[S] are reducible. We also exhibited an an algebraic expression that allows us to count irreducible polynomials in k[S] for k=Z/2Z (integers modulo 2) and S=<2,3> that relies on Mobius Inversion.
In this work we initiated the study of atomic density in numerical semigroup algebras, which is the limiting value of the ratio of irreducibles of degree n to total polynomials of degree n for some numerical semigroup algebra over a finite field. Numerical semigroup algebras exhibit non unique factorization, and it is of interest to see what is happening to the number of irreducibles of a given degree n as n grows larger. The main result of this paper is that any numerical semigroup algebra has atomic density 0. This means that for a given numerical semigroup algebra S over a finite field k, in some sense, `most' polynomials in k[S] are reducible. We also exhibited an an algebraic expression that allows us to count irreducible polynomials in k[S] for k=Z/2Z (integers modulo 2) and S=<2,3> that relies on Mobius Inversion.
Amicable Pairs

Amicable pairs, or friendly numbers, in the natural numbers are a pair of distinct positive integers (m,n) where each integer is the sum of the proper divisors of the other integer. The smallest amicable pair is is the pair (220,284). In this case we see that the proper divisors of 220--1,2,4,5,10,11,20,22,44,55,110, sum to 284, and the proper divisors of 284--1,2,4,71,142, sum to 220. This pair was known by the Greek as early as 300 BCE, and until 1750 there were only three known amicable pairs. In 1750, Euler discovered 58 more amicable pairs by considering pairs of a certain form. This set the stage for classifying amicable pairs according to type based on the factorization of each number in the pair. For example, since 220=2^2*5*11 and 284=2^2*71, the pair (220,284) is called a (2,1) pair, as 220 has two factors, and 284 has one factor outside of their common factor of 2^2.
There are now more than 1.2 billion known amicable pairs. The characterization of amicable pairs by type allows for searches for pairs using computer algorithms. It is unproven, but believed that there are infinitely many amicable pairs. The distribution of amicable pairs within the natural numbers has been studied, and upper bounds have been established for A(x), the number of amicable numbers in [1,x]. Amicable pairs have also been studied under the view of function iteration. An aliquot sequence is a sequence of positive integers where each term is the sum of the proper divisors of the previous term. An amicable pair is an aliquot sequence with a cycle of length two, sociable numbers are cycles of length greater than two, and a perfect number has a repeating aliquot cycle of length one. The Catalan-Dickson conjecture says that all aliquot sequences either terminate or are eventually periodic.
There are now more than 1.2 billion known amicable pairs. The characterization of amicable pairs by type allows for searches for pairs using computer algorithms. It is unproven, but believed that there are infinitely many amicable pairs. The distribution of amicable pairs within the natural numbers has been studied, and upper bounds have been established for A(x), the number of amicable numbers in [1,x]. Amicable pairs have also been studied under the view of function iteration. An aliquot sequence is a sequence of positive integers where each term is the sum of the proper divisors of the previous term. An amicable pair is an aliquot sequence with a cycle of length two, sociable numbers are cycles of length greater than two, and a perfect number has a repeating aliquot cycle of length one. The Catalan-Dickson conjecture says that all aliquot sequences either terminate or are eventually periodic.
Selected Works
Gaussian Amicable Pairs (with Patrick Costello)
The complex sum of divisors function was introduced by R. Spira as a natural extension of the standard sum of divisors function on the real numbers to the Gaussian integers. Using it, we can study how many properties characterized by the sum of divisors function extend to the Gaussian integers. In we extended the study of amicable pairs to the complex numbers. We answered the open question of whether Gaussian amicable pairs existed. We found over 100 new Gaussian amicable pairs with a complex part. We used Mathematica to search for pairs of certain types. We also identified classes of amicable pairs in the natural numbers that are also amicable when viewed as Gaussian integers and showed there are no (2,1) pairs in the integers, such as (220,284), that are also Gaussian amicable pairs.
This work just the tip of the iceberg, there is much left to be done in the exploration of Gaussian amicable numbers! If you are a student looking for a research experience please reach out if this program interests you.
The complex sum of divisors function was introduced by R. Spira as a natural extension of the standard sum of divisors function on the real numbers to the Gaussian integers. Using it, we can study how many properties characterized by the sum of divisors function extend to the Gaussian integers. In we extended the study of amicable pairs to the complex numbers. We answered the open question of whether Gaussian amicable pairs existed. We found over 100 new Gaussian amicable pairs with a complex part. We used Mathematica to search for pairs of certain types. We also identified classes of amicable pairs in the natural numbers that are also amicable when viewed as Gaussian integers and showed there are no (2,1) pairs in the integers, such as (220,284), that are also Gaussian amicable pairs.
This work just the tip of the iceberg, there is much left to be done in the exploration of Gaussian amicable numbers! If you are a student looking for a research experience please reach out if this program interests you.
Contact Me
|
|
addressThe Ohio State University
Department of Mathematics 231 W. 18th Ave., 700 MW Columbus, OH 43210 |
social |